UN3079 习题课 1 - 欢迎！

习题课地点与时间：周一上午 9 点 (Havemeyer 320) 及周一晚上 6 点 (Havemeyer 320)。 助教：Lauren Schaffer (她/他们)；电子邮件*：lks2160@columbia.edu 办公时间：周二下午 5:30-6:30，Havemeyer 7 楼。

议程：

习题课计划：

本次习题课旨在巩固课堂概念并提供练习题，以帮助您完成作业、小测验和考试。每周我都会在 Courseworks 上发布一份包含简要笔记和问题的讲义。我们也可以一起完成作业题，您也可以自己完成讲义。

作业不计入成绩，但对于通过本课程至关重要。为了激励您完成作业，如果您通过电子邮件将您的作业发送给我，我将回复一套课本习题解答。根据我的时间安排，我可能会手写解答。这是基于荣誉系统，请避免将其传播给未完成作业的人。

出勤：

习题课出勤不计入您的最终成绩，但强烈建议参加。习题课是备考（考试计入成绩）的有用资源。您可以选择参加周一上午 9 点或晚上 6 点的 50 分钟课程。

第 16 章 - 介绍与理想气体

I. 理想气体定律

PV=nRT\begin{equation*} P V=n R T \tag{1} \end{equation*}

理想气体定律是一个状态方程，它描述了物理变量压强 PP、体积 VV、摩尔数 nn 和温度 TT 之间的相互关系。定义 Vˉ=Vn\bar{V}=\frac{V}{n} 为摩尔体积，我们也可以写成：

PVˉ=RT\begin{equation*} P \bar{V}=R T \tag{2} \end{equation*}

理想气体定律有两个关键假设：1) 粒子不相互作用，2) 粒子没有体积。

II. 范德华方程

在高压和低温下，气体不再表现出理想行为。在一级修正中，我们通过范德华方程考虑分子间相互作用：

(P+aVˉ2)(Vˉ−b)=RT\begin{equation*} \left(P+\frac{a}{\bar{V}^{2}}\right)(\bar{V}-b)=R T \tag{3} \end{equation*}

其中 aa 和 bb 是给定气体的范德华常数。a\boldsymbol{a} 解释了粒子间的吸引力（单位 dm6⋅bar⋅mol−2\mathrm{dm}^{6} \cdot \mathrm{bar} \cdot \mathrm{mol}^{-2}），b\boldsymbol{b} 解释了粒子的大小（单位 dm3⋅mol−1\mathrm{dm}^{3} \cdot \mathrm{mol}^{-1}）。

第 17 章 - 概率与玻尔兹曼因子

I. 概率与统计

在本课程中，我们将涉及概率，因此值得花一些时间了解基本概念。概率 pjp_{j} 是某一特定事件 jj 发生的可能性。

pj=NjN\begin{equation*} p_{j}=\frac{N_{j}}{N} \tag{1} \end{equation*}

j\boldsymbol{j} 被称为可能结果的“索引”（例如，正面与反面）。Nj\boldsymbol{N}_{\boldsymbol{j}} 是结果 jj 发生的次数。N\boldsymbol{N} 是事件的总次数。

问：假设我们抛一枚硬币。我们将使用索引 j=1j=1 表示正面结果， j=2j=2 表示反面结果。写出掷出正面 (p1p_{1}) 和反面 (p2p_{2}) 概率的一般表达式。

答：N1N_{1} 是我们得到正面的次数，N2N_{2} 是我们得到反面的次数。事件的总次数 NN 是我们抛掷硬币的次数，等于掷出正面或反面的次数之和：N=N1+N2N=N_{1}+N_{2}。因此

p1=N1N=N1N1+N2p2=N2N=N2N1+N2\begin{aligned} & p_{1}=\frac{N_{1}}{N}=\frac{N_{1}}{N_{1}+N_{2}} \\ & p_{2}=\frac{N_{2}}{N}=\frac{N_{2}}{N_{1}+N_{2}} \end{aligned}

当我们将每个可能结果的概率之和设为 1 时，我们称该概率分布是归一化的：

∑j=1npj=1\begin{equation*} \sum_{j=1}^{n} p_{j}=1 \tag{2} \end{equation*}

其中 nn 是可能结果的总数。这告诉我们某事发生的概率是 1。以硬币为例，正面或反面是两个可能的结果，所以 n=2n=2。请参阅问题 5 了解其工作原理。

另一个有用的量是分布的均值 ⟨x⟩\langle\boldsymbol{x}\rangle，其中 xj\boldsymbol{x}_{\boldsymbol{j}} 是值（正面或反面，表示为 1 或 2），pj\boldsymbol{p}_{\boldsymbol{j}} 是概率（0.5 或 50%）。xx 是一个通用变量，可以替换为我们想要测量的任何物理可观测量。

⟨x⟩=∑j=1nxjpj\begin{equation*} \langle x\rangle=\sum_{j=1}^{n} x_{j} p_{j} \tag{3} \end{equation*}

σx2\boldsymbol{\sigma}_{\boldsymbol{x}}^{\mathbf{2}} 是方差，它衡量 xx 值与均值相差的程度（它们与平均值的离散程度）。σx2\sigma_{x}^{2} 定义为：

σx2=⟨(x−⟨x⟩)2⟩=∑j=1n(xj−⟨x⟩)2pj\begin{equation*} \sigma_{x}^{2}=\left\langle(x-\langle x\rangle)^{2}\right\rangle=\sum_{j=1}^{n}\left(x_{j}-\langle x\rangle\right)^{2} p_{j} \tag{4} \end{equation*}

方差的平方根称为标准差 σx\boldsymbol{\sigma}_{x}，这可能更熟悉：

σx=σx2=⟨(x−⟨x⟩)⟩=∑j=1n(x−⟨x⟩)pj\begin{equation*} \sigma_{x}=\sqrt{\sigma_{x}^{2}}=\langle(x-\langle x\rangle)\rangle=\sum_{j=1}^{n}(x-\langle x\rangle) p_{j} \tag{5} \end{equation*}

利用我们对概率的理解，我们可以描述在某些激发态中找到粒子的概率。量子力学（物理化学 II）的一个关键见解告诉我们，原子和分子的允许能态是离散的或非连续的。例如，我们可能想知道有多少分子处于振动基态或第一激发振动态。

II. 玻尔兹曼因子

玻尔兹曼因子是热力学中一个极其有用的工具，它将系统处于某个能量状态的概率与其能量和温度联系起来。玻尔兹曼因子告诉我们，系统处于能量为 Ej(j=1,2,3…)\boldsymbol{E}_{\boldsymbol{j}} (j=1,2,3\ldots) 的状态的概率 pj\boldsymbol{p}_{\boldsymbol{j}} 随能量 EjE_{j} 指数衰减：

pj∝e−EjkBT\begin{equation*} p_{j} \propto e^{-\frac{E_{j}}{k_{B} T}} \tag{6} \end{equation*}

其中 kBk_{B} 是玻尔兹曼常数，kB=1.38×10−23JK=RNAk_{B}=1.38 \times 10^{-23} \frac{J}{K}=\frac{R}{N_{A}}。从定性上讲，公式 (6) 告诉我们，高能态比低能态更不容易被占据。

问：证明在恒定温度 TT 下，分子处于状态 EjE_{j} 的概率 pjp_{j} 随着索引 jj 的增加而指数式减小。此外，证明对于给定的能态 EjE_{j}，在较高温度下，较高能态更有可能被占据（反之，在较低温度下，较低能态更有可能被占据）。

答：我们已经将玻尔兹曼因子绘制成能量 EjE_{j} 的函数，分别在三个温度下：T=100 K,200 K,300 KT=100 \mathrm{~K}, 200 \mathrm{~K}, 300 \mathrm{~K}。我们可以看到 TT 的值决定了指数衰减的速率。在较高的 TT 下，指数项 e−EjkBTe^{-\frac{E_{j}}{k_{B} T}} 衰减得更慢。

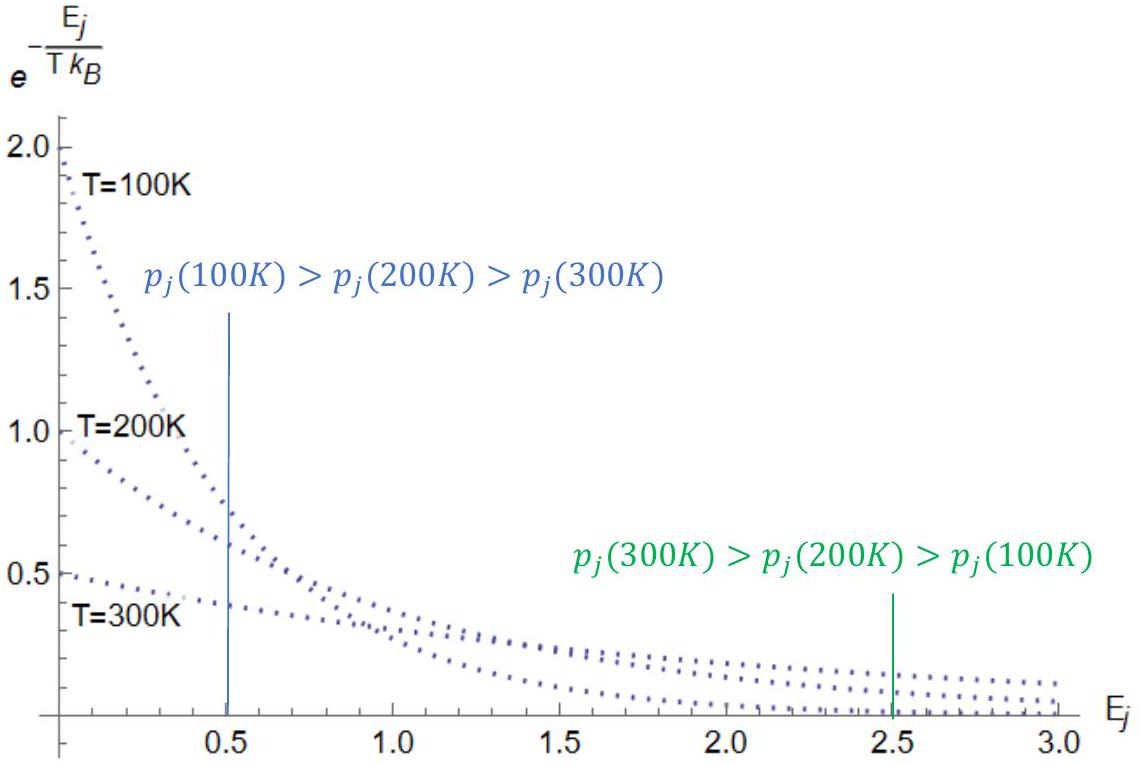
对于问题的第二部分，比较在 Ej=0.5E_{j}=0.5 处三个温度的 pj∝e−EjkBTp_{j} \propto e^{-\frac{E_{j}}{k_{B} T}}。我们看到 pj(100K)>pj(200K)>pj(300K)p_{j}(100 K)>p_{j}(200 K)>p_{j}(300 K)。这意味着这个特定的状态 (Ej=0.5E_{j}=0.5) 在较低温度下被占据的可能性更大。在较高能态 Ej=2.5E_{j}=2.5 处，趋势则相反，这意味着较高能态在较高温度下更有可能被占据。这应该很直观。

此外，通常方便定义量 β=1kBT\boldsymbol{\beta}=\frac{\mathbf{1}}{\boldsymbol{k}_{\boldsymbol{B}} \boldsymbol{T}}，这样我们可以更简洁地写出玻尔兹曼因子：

pj∝e−βEj\begin{equation*} p_{j} \propto e^{-\beta E_{j}} \tag{7} \end{equation*}

较小的 β\beta 对应较高的温度和较慢的衰减。较大的 β\beta 对应较低的温度和较快的衰减。

III. 配分函数

让我们回顾第一部分的归一化概率，我们将单个事件 NjN_{j} 除以可能结果的总数 NN，使得 pj=NjNp_{j}=\frac{N_{j}}{N} (1) 且 ∑j=1npj=1\sum_{j=1}^{n} p_{j}=1 (2)。现在，我们可以将每个事件 NjN_{j} 视为不同的状态，将所有可能结果的总和 NN 视为状态总数。

如果我们想将概率和 pj∝e−βEjp_{j} \propto e^{-\beta E_{j}} 归一化为 1，我们需要引入一个归一化因子，该因子对系统可以占据的所有可能状态求和。这个归一化因子称为配分函数，用 Q\mathbf{Q} 表示：

Q=∑ie−βEi\begin{equation*} Q=\sum_{i} e^{-\beta E_{i}} \tag{8} \end{equation*}

其中 ii 是求和的索引。这个和是对所有可能的状态进行的。配分函数极其强大，因为它包含了系统每个可能状态的相对能量信息。我们以后将使用它来计算各种系统的平均宏观热力学量，例如热容、能量和压强。

类比地，

Nj→e−βEjN→Q\begin{gathered} N_{j} \rightarrow e^{-\beta E_{j}} \\ N \rightarrow Q \end{gathered}

因此，我们将粒子（即原子或分子）处于某个能量状态 EjE_{j} 的概率写为：

pj=e−βEjQ=e−βEj∑ie−βEi\begin{equation*} p_{j}=\frac{e^{-\beta E_{j}}}{Q}=\frac{e^{-\beta E_{j}}}{\sum_{i} e^{-\beta E_{i}}} \tag{9} \end{equation*}

注意变量依赖性 Q( N, V, T)Q(\mathrm{~N}, \mathrm{~V}, \mathrm{~T}) 或 Q( N, V,β)Q(\mathrm{~N}, \mathrm{~V}, \beta)，而能量 Ej( N, V)E_{j}(\mathrm{~N}, \mathrm{~V})。N 是分子数，V 是体积，T 是温度。

在本课程后期，当我们将讨论相变和化学反应中能量被吸收/释放而温度保持恒定（例如冰融化）时，这个概念将变得清晰。

供您参考，能量分布的均值（平均能量）可以用 QQ 定义为：

⟨E⟩=−∂ln⁡Q∂β\begin{equation*} \langle E\rangle=-\frac{\partial \ln Q}{\partial \beta} \tag{10} \end{equation*}

这将在我们课程的进展中派上用场。

问题

Q1

在什么实验条件下，理想气体定律是一个很好的近似？

Q2

证明当样品极度稀释（即 Vˉ\bar{V} 很大）时，范德华方程 (3) 简化为理想气体定律 (1)。

Q3

(理想气体定律 - 改编自 16.10) 将 1 升 2.1 bar 的 N2( g)\mathrm{N}_{2(\mathrm{~g})} 和 2 升 3.4 bar 的 Ar⁡(g)\operatorname{Ar}_{(\mathrm{g})} 混合在一个 4.0 升的烧瓶中，形成理想气体混合物。假设气体行为理想。 a. 如果 N2( g)\mathrm{N}_{2(\mathrm{~g})} 和 Ar(g)\mathrm{Ar}_{(\mathrm{g})} 气体的初始和最终温度相同，计算混合物的最终压强。 i. 使用理想气体定律确定每种气体的摩尔数。回想 1 L=1×10−3 m31 \mathrm{~L}=1 \times 10^{-3} \mathrm{~m}^{3} 和 1bar=1×105 Pa1 \mathrm{bar}=1 \times 10^{5} \mathrm{~Pa}。（提示：将 RTRT 保留为变量）。 ii. 使用气体的总摩尔数和理想气体定律确定混合物的最终压强。 b. 如果 N2( g)\mathrm{N}_{2(\mathrm{~g})} 和 Ar(g)\mathrm{Ar}_{(\mathrm{g})} 的初始温度分别为 304 K 和 402 K，且混合物的最终温度为 377 K，计算混合物的最终压强。 i. 现在我们将在计算中包含温度。确定每种气体的摩尔数（将 RR 保留为变量）。 ii. 使用新的气体总摩尔数和理想气体定律确定混合物的最终压强。

Q4

概率与归一化。假设我们抛一枚硬币 20 次。我们掷出 8 次正面 (N1=8N_{1}=8) 和 12 次反面 (N2=12N_{2}=12)。根据这组数据，掷出正面与反面的概率分别是多少？证明掷出正面或反面的概率是归一化的。

Q5

平均能量： a. 首先，假设一个系统只有两个能级 E1E_{1} 和 E2E_{2}。写出该系统的配分函数。 b. 写出该系统的平均能量。这可以通过两种方式完成。 c. 现在考虑一个具有 jj 个状态，能量分别为 E1,E2,…EjE_{1}, E_{2}, \ldots E_{j} 的系统。写出配分函数以及用 QQ 表示的具有 jj 个状态的系统平均能量 ⟨E⟩\langle E\rangle 的通用表达式。在您的表达式中包含 QQ 和 EjE_{j} 的变量依赖性。

Q6

4D 单原子理想气体的平均能量和热容：理想气体和许多其他不可分辨粒子的系统的配分函数可以表示为单个原子或分子配分函数的乘积：

Q=qNN!Q=\frac{q^{N}}{N!}

其中 qq 是单个粒子（即原子或分子）的配分函数。请参阅课本第 17-8 节（第 713 页），了解配分函数的分解。我们将用它来计算系统的平均能量 ⟨E⟩\langle E\rangle 和热容 CVC_{V}。 a. 利用 4D 单原子气体的以下表达式：

q=(2πmkBTh2)2Vq=\left(\frac{2 \pi m k_{B} T}{h^{2}}\right)^{2} V

写出 QQ 的表达式。 b. 使用以下关系（在课本第 698 页推导），以 N,kBN, k_{B} 和 TT 表示平均能量 ⟨E⟩\langle E\rangle。

⟨E⟩=kBT2(∂ln⁡Q∂T)N,V\langle E\rangle=k_{B} T^{2}\left(\frac{\partial \ln Q}{\partial T}\right)_{N, V}

i. 代入您对 QQ 的表达式并展开自然对数。 ii. 对您的表达式 ∂ln⁡Q∂T\frac{\partial \ln Q}{\partial T} 关于 TT 求偏导数并简化以获得 ⟨E⟩\langle E\rangle。 c. 使用 ⟨E⟩\langle E\rangle 和定容热容 CVC_{V} 的定义：

CV=(∂⟨E⟩∂T)N,VC_{V}=\left(\frac{\partial\langle E\rangle}{\partial T}\right)_{N, V}

写出 4D 单原子理想气体的热容。